公理化体系和不完备性定理
最早在 19 世纪初,德国著名数学家希尔伯特提出:这个世界可以建立一套完善的公理体系,由少数几个公理出发,推导出所有的定理和推论。这样就可以逐渐通过这种方法将世界上的万事万物都统一到一个体系中。
当然,这只是一个非常美好的设想,如果万事万物都可以用形式化(简单理解就是程序化规范化)的手段统一到一套体系中,也就意味着计算能力将被无限扩展,只要给定足够的时间和空间,计算机就可以完成任何工作。
但在不久后,美籍数学家哥德尔就提出了哥德尔不完备性定理,内容是:即便在完善的公理体系中仍然可以找到不能被证明也不能被证伪的命题。
这让我联想到,一说谎,鼻子就会变长的匹诺曹。如果他说“我说谎了”,那么他的鼻子应该变长还是变短呢?对于人类而言,这个问题可以理解,但是对于计算机来说这个问题是不可以被计算的。
正是因为世界上存在着大量的这种“公说公有理,婆说婆有理”的问题,才让大家认识到计算不能解决所有问题,所以:计算机能力也是有边界的。哥德尔的不完备性定理,让大家看到了世界上还有大量不可计算的问题。
从极限的角度看,人工智能是万能的么?
- 人工智能是计算机的一个应用。计算机不是万能的,人工智能自然也不是。
常人想问题的方式:
- 先做一两个能解决简单问题的计算机,然后越做越复杂。
- 工匠式的:从量变到质变。
- 迭代式进步,小步快跑。
- 认识数字,从 1,2,3,一直到 100。
图灵想问题和常人相反,思考三个问题:
- 世界上是否所有数学问题都有明确地答案。
- 如果有明确地答案,是否可以通过有限步骤的计算得到答案。
- 对于那些有可能在有限步骤计算出来的数学问题,能否有一种假想的机械,让它不断运动,最后当机器停下来的时候,那个数学问题就解决了?
图灵和常人思维的差别:
- 先找极限,再在极限中寻求答案。不浪费世界纠结在试图超越极限的事情上。
图灵机:
- 划定范围。
- 设计有效且通用的办法。
- 保证按照这个办法做事,最终找到答案。
人工智能的边界:
- 世界上很多问题,只有一小部分是数学问题。
- 在数学问题中,只有一小部分是有解的。
- 在有解问题中,只有一部分是理想状态的图灵机可以解决的。
- 在后一类问题中,只有一部分是今天实际的计算机可以解决的。
- 而人工智能可以解决的问题,又知识计算机可以解决问题的一部分。
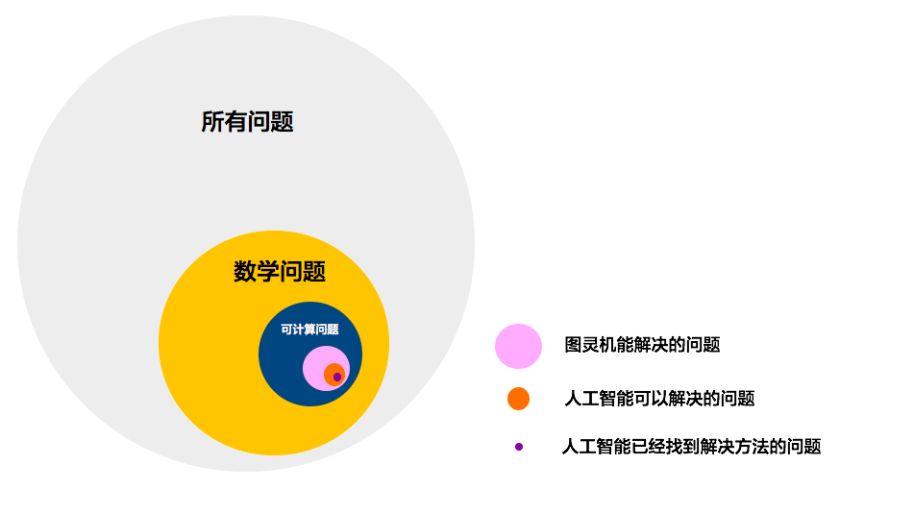 问题的分类
问题的分类
图灵机和可计算理论
于是人们意识到了需要一个理论,专门回答这样的问题:哪些问题可以被计算,哪些不可以被计算,这就是可计算性理论,该理论是计算机科学的理论基础之一。
1936 年,被誉为人工智能之父的阿兰·图灵提出了图灵机,它是一种不断执行指令的抽象计算机。之所以说抽象,是因为图灵并没有真的造出这台机器,而是把它当成理论去和大家探讨可计算问题。
图灵发现如果一个问题是可计算的,那么它的解决方案就必须可以被具化成一条条的指令,也就是可以使用图灵机处理。因此,不能使用图灵机处理的问题,都是不可计算的问题。
比如一个马达的控制程序是可计算的,因为控制过程是可以被抽象成一条条指令的(即可以写程序实现)。比如程序可以先读入传感器的数据,然后根据数据计算出下面要进行加速还是减速。
在计算机的世界中,有两位巨擘对问题的可计算性做了模型化描述
1、阿兰.图灵(Alan Turing),他提出的图灵机。计算机系的各种学科中都充斥着这个概念,假设有一个纸带和一个打孔机,然后有一套指令,能够控制打孔机在纸带上移动、能够读取当前位置是否打了孔、能够在当前位置打一个孔,这就是一个图灵机,假设一个问题能够靠这个纸带+打孔机+指令的方式解决,那就说明这个问题是“可计算的”。
2、阿隆佐·邱奇(Alonzo Church)。邱奇是个数学家,他提出了Lambda演算(Lambda Calculus)的概念,用函数组合的方式来描述计算过程,换句话来说,如果一个问题能够用一套函数组合的算法来表达,那就说明这个问题是可计算的。
引用别人的理解:
1、图灵机是通过一系列指令和状态来完成某种过程的,即,在某种状态下使用怎样的指令转移到某种状态。
2、Lambda演算是通过一个函数来解决这个问题,而这个函数又是由一系列别的函数组成,这样递归下去,最终达到常量。有些类似动态规划那种一个问题由多个子问题组成,子问题又有自己的子问题,最后到达一些已知解的问题。
3、不是全部的Lambda演算思想都可以运用到实际中,因Lambda演算在设计的时候就不是为了在各种现实世界中的限制下工作的。
